Capillary electrophoresis
| Acronym | CE |
|---|---|
| Classification | Electrophoresis |
| Analytes | Biomolecules Chiral molecules |
| Other techniques | |
| Related | gel electrophoresis Two-dimensional gel electrophoresis |
| Hyphenated | Capillary electrophoresis mass spectrometry |
Capillary electrophoresis (CE), also known as capillary zone electrophoresis (CZE), can be used to separate ionic species by their charge and frictional forces and hydrodynamic radius. In traditional electrophoresis, electrically charged analytes move in a conductive liquid medium under the influence of an electric field. Introduced in the 1960s, the technique of capillary electrophoresis (CE) was designed to separate species based on their size to charge ratio in the interior of a small capillary filled with an electrolyte.
Contents |
Instrumentation
The instrumentation needed to perform capillary electrophoresis is relatively simple. A basic schematic of a capillary electrophoresis system is shown in Figure 1. The system's main components are a sample vial, source and destination vials, a capillary, electrodes, a high-voltage power supply, a detector, and a data output and handling device. The source vial, destination vial and capillary are filled with an electrolyte such as an aqueous buffer solution. To introduce the sample, the capillary inlet is placed into a vial containing the sample and then returned to the source vial (sample is introduced into the capillary via capillary action, pressure, or siphoning). The migration of the analytes is then initiated by an electric field that is applied between the source and destination vials and is supplied to the electrodes by the high-voltage power supply. It is important to note that all ions, positive or negative, are pulled through the capillary in the same direction by electroosmotic flow, as will be explained. The analytes separate as they migrate due to their electrophoretic mobility, as will be explained, and are detected near the outlet end of the capillary. The output of the detector is sent to a data output and handling device such as an integrator or computer. The data is then displayed as an electropherogram, which reports detector response as a function of time. Separated chemical compounds appear as peaks with different migration times in an electropherogram.[1]
Detection
Separation by capillary electrophoresis can be detected by several detection devices. The majority of commercial systems use UV or UV-Vis absorbance as their primary mode of detection. In these systems, a section of the capillary itself is used as the detection cell. The use of on-tube detection enables detection of separated analytes with no loss of resolution. In general, capillaries used in capillary electrophoresis are coated with a polymer for increased stability. The portion of the capillary used for UV detection, however, must be optically transparent. Bare capillaries can break relatively easily and, as a result, capillaries with transparent coatings are available to increase the stability of the cell window. The path length of the detection cell in capillary electrophoresis (~ 50 micrometers) is far less than that of a traditional UV cell (~ 1 cm). According to the Beer-Lambert law, the sensitivity of the detector is proportional to the path length of the cell. To improve the sensitivity, the path length can be increased, though this results in a loss of resolution. The capillary tube itself can be expanded at the detection point, creating a "bubble cell" with a longer path length or additional tubing can be added at the detection point as shown in figure 2. Both of these methods, however, will decrease the resolution of the separation.[2]
Fluorescence detection can also be used in capillary electrophoresis for samples that naturally fluoresce or are chemically modified to contain fluorescent tags. This mode of detection offers high sensitivity and improved selectivity for these samples, but cannot be utilized for samples that do not fluoresce. The set-up for fluorescence detection in a capillary electrophoresis system can be complicated. The method requires that the light beam be focused on the capillary, which can be difficult for many light sources.[2] Laser-induced fluorescence has been used in CE systems with detection limits as low as 10−18 to 10−21 mol. The sensitivity of the technique is attributed to the high intensity of the incident light and the ability to accurately focus the light on the capillary.[1]
In order to obtain the identity of sample components, capillary electrophoresis can be directly coupled with mass spectrometers or Surface Enhanced Raman Spectroscopy (SERS). In most systems, the capillary outlet is introduced into an ion source that utilizes electrospray ionization (ESI). The resulting ions are then analyzed by the mass spectrometer. This set-up requires volatile buffer solutions, which will affect the range of separation modes that can be employed and the degree of resolution that can be achieved.[2] The measurement and analysis are mostly done with a specialized gel analysis software.
For CE-SERS, capillary electrophoresis eluants can be deposited onto a SERS-active substrate. Analyte retention times can be translated into spatial distance by moving the SERS-active substrate at a constant rate during capillary electrophoresis. This allows the subsequent spectroscopic technique to be applied to specific eluants for identification with high sensitivity. SERS-active substrates can be chosen that do not interfere with the spectrum of the analytes.[3]
Modes of separation
The separation of compounds by capillary electrophoresis is dependent on the differential migration of analytes in an applied electric field. The electrophoretic migration velocity (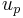 ) of an analyte toward the electrode of opposite charge is:
) of an analyte toward the electrode of opposite charge is:
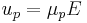
where 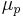 is the electrophoretic mobility and E is the electric field strength. The electrophoretic mobility is proportional to the ionic charge of a sample and inversely proportional to any frictional forces present in the buffer. When two species in a sample have different charges or experience different frictional forces, they will separate from one another as they migrate through a buffer solution. The frictional forces experienced by an analyte ion depend on the viscosity (η) of the medium and the size and shape of the ion.[2] Accordingly, the electrophoretic mobility of an analyte at a given pH is given by:
is the electrophoretic mobility and E is the electric field strength. The electrophoretic mobility is proportional to the ionic charge of a sample and inversely proportional to any frictional forces present in the buffer. When two species in a sample have different charges or experience different frictional forces, they will separate from one another as they migrate through a buffer solution. The frictional forces experienced by an analyte ion depend on the viscosity (η) of the medium and the size and shape of the ion.[2] Accordingly, the electrophoretic mobility of an analyte at a given pH is given by:
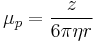
where 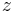 is the net charge of the analyte and
is the net charge of the analyte and  is the Stokes radius of the analyte. The Stokes radius is given by:
is the Stokes radius of the analyte. The Stokes radius is given by:
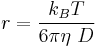
where 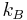 is the Boltzmann constant, and
is the Boltzmann constant, and  is the temperature, D is the diffusion coefficient. These equations indicate that the electrophoretic mobility of the analyte is proportional to the charge of the analyte and inversely proportional to its radius. The electrophoretic mobility can be determined experimentally from the migration time and the field strength:
is the temperature, D is the diffusion coefficient. These equations indicate that the electrophoretic mobility of the analyte is proportional to the charge of the analyte and inversely proportional to its radius. The electrophoretic mobility can be determined experimentally from the migration time and the field strength:
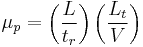
where  is the distance from the inlet to the detection point,
is the distance from the inlet to the detection point, 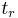 is the time required for the analyte to reach the detection point (migration time),
is the time required for the analyte to reach the detection point (migration time),  is the applied voltage (field strength), and
is the applied voltage (field strength), and 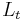 is the total length of the capillary.[2] Since only charged ions are affected by the electric field, neutral analytes are poorly separated by capillary electrophoresis.
is the total length of the capillary.[2] Since only charged ions are affected by the electric field, neutral analytes are poorly separated by capillary electrophoresis.
The velocity of migration of an analyte in capillary electrophoresis will also depend upon the rate of electroosmotic flow (EOF) of the buffer solution. In a typical system, the electroosmotic flow is directed toward the negatively charged cathode so that the buffer flows through the capillary from the source vial to the destination vial. Separated by differing electrophoretic mobilities, analytes migrate toward the electrode of opposite charge.[1] As a result, negatively charged analytes are attracted to the positively charged anode, counter to the EOF, while positively charged analytes are attracted to the cathode, in agreement with the EOF as depicted in figure 3.
The velocity of the electroosmotic flow, 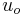 can be written as:
can be written as:
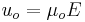
where 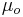 is the electroosmotic mobility, which is defined as:
is the electroosmotic mobility, which is defined as:
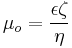
where 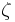 is the zeta potential of the capillary wall, and
is the zeta potential of the capillary wall, and  is the relative permittivity of the buffer solution. Experimentally, the electroosmotic mobility can be determined by measuring the retention time of a neutral analyte.[2] The velocity (
is the relative permittivity of the buffer solution. Experimentally, the electroosmotic mobility can be determined by measuring the retention time of a neutral analyte.[2] The velocity ( ) of an analyte in an electric field can then be defined as:
) of an analyte in an electric field can then be defined as:
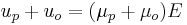
Since the electroosmotic flow of the buffer solution is generally greater than that of the electrophoretic flow of the analytes, all analytes are carried along with the buffer solution toward the cathode. Even small, triply charged anions can be redirected to the cathode by the relatively powerful EOF of the buffer solution. Negatively charged analytes are retained longer in the capillary due to their conflicting electrophoretic mobilities.[1] The order of migration seen by the detector is shown in figure 3: small multiply charged cations migrate quickly and small multiply charged anions are retained strongly.[2]
Electroosmotic flow is observed when an electric field is applied to a solution in a capillary that has fixed charges on its interior wall. Charge is accumulated on the inner surface of a capillary when a buffer solution is placed inside the capillary. In a fused-silica capillary, silanol (Si-OH) groups attached to the interior wall of the capillary are ionized to negatively charged silanoate (Si-O-) groups at pH values greater than three. The ionization of the capillary wall can be enhanced by first running a basic solution, such as NaOH or KOH through the capillary prior to introducing the buffer solution. Attracted to the negatively charged silanoate groups, the positively charged cations of the buffer solution will form two inner layers of cations (called the diffuse double layer or the electrical double layer) on the capillary wall as shown in figure 4. The first layer is referred to as the fixed layer because it is held tightly to the silanoate groups. The outer layer, called the mobile layer, is farther from the silanoate groups. The mobile cation layer is pulled in the direction of the negatively charged cathode when an electric field is applied. Since these cations are solvated, the bulk buffer solution migrates with the mobile layer, causing the electroosmotic flow of the buffer solution. Other capillaries including Teflon capillaries also exhibit electroosmotic flow. The EOF of these capillaries is probably the result of adsorption of the electrically charged ions of the buffer onto the capillary walls.[1] The rate of EOF is dependent on the field strength and the charge density of the capillary wall. The wall's charge density is proportional to the pH of the buffer solution. The electroosmotic flow will increase with pH until all of the available silanols lining the wall of the capillary are fully ionized.[2]
Efficiency and resolution
The number of theoretical plates, or separation efficiency, in capillary electrophoresis is given by:
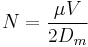
where  is the number of theoretical plates,
is the number of theoretical plates,  is the apparent mobility in the separation medium and
is the apparent mobility in the separation medium and 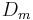 is the diffusion coefficient of the analyte. According to this equation, the efficiency of separation is only limited by diffusion and is proportional to the strength of the electric field. The efficiency of capillary electrophoresis separations is typically much higher than the efficiency of other separation techniques like HPLC. Unlike HPLC, in capillary electrophoresis there is no mass transfer between phases.[2] In addition, the flow profile in EOF-driven systems is flat, rather than the rounded laminar flow profile characteristic of the pressure-driven flow in chromatography columns as shown in figure 5. As a result, EOF does not significantly contribute to band broadening as in pressure-driven chromatography. Capillary electrophoresis separations can have several hundred thousand theoretical plates.[4]
is the diffusion coefficient of the analyte. According to this equation, the efficiency of separation is only limited by diffusion and is proportional to the strength of the electric field. The efficiency of capillary electrophoresis separations is typically much higher than the efficiency of other separation techniques like HPLC. Unlike HPLC, in capillary electrophoresis there is no mass transfer between phases.[2] In addition, the flow profile in EOF-driven systems is flat, rather than the rounded laminar flow profile characteristic of the pressure-driven flow in chromatography columns as shown in figure 5. As a result, EOF does not significantly contribute to band broadening as in pressure-driven chromatography. Capillary electrophoresis separations can have several hundred thousand theoretical plates.[4]
The resolution (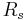 ) of capillary electrophoresis separations can be written as:
) of capillary electrophoresis separations can be written as:
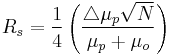
According to this equation, maximum resolution is reached when the electrophoretic and electroosmotic mobilities are similar in magnitude and opposite in sign. In addition, it can be seen that high resolution requires lower velocity and, correspondingly, increased analysis time.[2]
Related techniques
As discussed above, separations in a capillary electrophoresis system are typically dependent on the analytes having different electrophoretic mobilities. However, some classes of analyte cannot be separated by this effect because they are neutral (uncharged) or because they may not differ significantly in electrophoretic mobility. However, there are several techniques that can help separate such analytes with a capillary electrophoresis system. Adding a surfactant to the electrolyte can facilitate the separation of neutral compounds by micellar electrokinetic chromatography. Charged polymers such as DNA can be separated by filling the capillary with a gel matrix that retards longer strands more than shorter strands. This is called capillary gel electrophoresis. This is a high-resolution alternative to slab gel electrophoresis. Some capillary electrophoresis systems can also be used for microscale liquid chromatography or capillary electrochromatography. A capillary electrophoresis system can also be used for isotachophoresis, isoelectric focusing, and affinity electrophoresis. In the case of amino acid separations, the ion charge ranges from -1 to -3 electrons but the size of the amino acid is dominated by the dye label; therefore changes in charge have a significant effect on mobility relative to changes in size.
See also
- Affinity electrophoresis
- DNA Separation by Silica Adsorption
- Label-free HPCE Systems
- Kinetic capillary electrophoresis
References
- ^ a b c d e f Skoog, D.A.; Holler, F.J.; Crouch, S.R "Principles of Instrumental Analysis" 6th ed. Thomson Brooks/Cole Publishing: Belmont, CA 2007.
- ^ a b c d e f g h i j Skoog, D.A.; Holler, F.J.; Crouch, S.R "Principles of Instrumental Analysis" 6th ed. Chapter 30 Thomson Brooks/Cole Publishing: Belmont, CA 2007.
- ^ Lin H.; Natan, M.; Keating, C. Anal. Chem. 2000, 72, 5348-5355.
- ^ Skoog, D.A.; Holler, F.J.; Nieman, T.A. "Principles of Instrumental Analysis, 5th ed." Saunders college Publishing: Philadelphia, 1998.
Bibliography
- Terabe, S.; Otsuka, K.; Ichikawa, K.; Tsuchiya, A.; Ando, T. Anal. Chem. 1984, 56, 111.
- Terabe, S.; Otsuka, K.; Ichikawa, K.; Tsuchiya, A.; Ando, T. Anal. Chem. 1984, 56, 113.
- Foley, J.P. Anal. Chem. 1990, 62, 1302.
- Carretero, A.S.; Cruces-Blanco, C.; Ramirez, S.C.; Pancorbo, A.C.; Gutierrez, A.F. J. Agric. Food. Chem. 2004, 52, 5791.
- Cavazza, A.; Corradini, C.; Lauria, A.; Nicoletti, I. J. Agric. Food Chem. 2000, 48, 3324.
- Rodrigues, M.R.A.; Caramao, E.B.; Arce, L.; Rios, A.; Valcarcel, M. J. Agric. Food Chem. 2002, 50, 4215.